![]() Samstag, 9. August 2025, 17:53 UTC+2
Samstag, 9. August 2025, 17:53 UTC+2
Sie sind nicht angemeldet.
 Youngbiker.de Forum - Community & Infos für 125er, Sportler, Enduros, Supermotos, Tourer, Chopper und Cruiser »
Youngbiker.de Forum - Community & Infos für 125er, Sportler, Enduros, Supermotos, Tourer, Chopper und Cruiser » Other »
Other » Talk »
Talk »
Registrierungsdatum: 24. September 2003
Bike: Honda CBZ 125 F, Kawasaki GPZ 500S '98
Wohnort: Irgendwo in NRW
Mathereferat über die geometrische Bedeutung vom Skalarprodukt
Hallo ihrs!
Ich muss ein Referat für den MatheLK über die geometrische Bedeutung des Skalarprodukts halten, jedoch weiss ich nicht so ganz, wie ich das erläutern soll.
Gegeben ist die Gleichung: u*v = |u|·|v| cos phi "u" und "v" sind Vektoren.
Dazu müsste ich jetzt noch die Herleitung wissen, damit ich dem Kurs irgendwie erklären kann, wie man auf diese Gleichung kommt.
Hat von euch jemand Ahnung davon und kann mir ein wenig behilflich sein?
Vielen Dank schonmal im Vorraus!
Lucas.
Ich muss ein Referat für den MatheLK über die geometrische Bedeutung des Skalarprodukts halten, jedoch weiss ich nicht so ganz, wie ich das erläutern soll.
Gegeben ist die Gleichung: u*v = |u|·|v| cos phi "u" und "v" sind Vektoren.
Dazu müsste ich jetzt noch die Herleitung wissen, damit ich dem Kurs irgendwie erklären kann, wie man auf diese Gleichung kommt.
Hat von euch jemand Ahnung davon und kann mir ein wenig behilflich sein?
Vielen Dank schonmal im Vorraus!
Lucas.
Du musst!
Registrierungsdatum: 24. September 2003
Bike: Honda CBZ 125 F, Kawasaki GPZ 500S '98
Wohnort: Irgendwo in NRW
Dort finde ich meistens nichts anderes als ich auch bei mir im Buch stehen habe. Nur steht nirgendwo geschrieben, wie man auf diese Gleichung kommt.
Ich muss den Schülern doch irgendwie erklären, warum diese Gleichung so sein mus wie sie ist.
Ich muss den Schülern doch irgendwie erklären, warum diese Gleichung so sein mus wie sie ist.
Du musst!
Das Skalarprodukt ist ursprünglich im Rahmen der analytischen Geometrie im euklidischen Raum eingeführt worden. So ist es mit Hilfe des Skalarproduktes beispielsweise möglich, den Winkel zwischen zwei Vektoren zu berechnen: Das Skalarprodukt ergibt sich nämlich auch aus den Beträgen der beiden Vektoren und dem Kosinus des von diesen eingeschlossenen Winkels gemäß der Formel
\vec{x}\cdot \vec{y} = |\vec{x} | \cdot | \vec{y} | \cdot \cos \measuredangle \left(\vec{x},\vec{y}\right)
Um dies zu zeigen, mögen drei Vektoren, \vec{a},\vec{b},\vec{c} des euklidischen Raumes betrachtet werden.
Bild kalarproduktSkizze.jpg
kalarproduktSkizze.jpg
Wegen des Kosinussatzes ist die Länge des dem Winkel ³ gegenüberliegenden Vektors
|\vec{c}|^2=|\vec{a}|^2+|\vec{b}|^2-2|\vec{a}||\vec{b}| \cdot \cos(\gamma)
Da sich \vec{c} als \vec{b}-\vec{a} ergibt, erhält man
|\vec{b}-\vec{a}|^2=|\vec{a}|^2+|\vec{b}|^2-2|\vec{a}||\vec{b}| \cdot \cos(\gamma).
Berechnet man nun die Länge über das Skalarprodukt, so erhält man
\left(\vec{b}-\vec{a}\right)\cdot\left(\vec{b}-\vec{a}\right) = \vec{a}\cdot\vec{a} + \vec{b}\cdot\vec{b}-2|\vec{a}||\vec{b}| \cdot \cos(\gamma).
Aus den Rechenregeln für das Skalarprodukt ergibt sich dann
\vec{b}\cdot\vec{b} -2 \vec{a}\cdot\vec{b}+ \vec{a}\cdot\vec{a} = \vec{a}\cdot\vec{a} + \vec{b}\cdot\vec{b}-2|\vec{a}||\vec{b}| \cdot \cos(\gamma)
und daraus die gewünschte Beziehung
\vec{a}\cdot\vec{b} = |\vec{a}||\vec{b}| \cdot \cos(\gamma).
ups--- liess ienfahc selber im wiki nach
\vec{x}\cdot \vec{y} = |\vec{x} | \cdot | \vec{y} | \cdot \cos \measuredangle \left(\vec{x},\vec{y}\right)
Um dies zu zeigen, mögen drei Vektoren, \vec{a},\vec{b},\vec{c} des euklidischen Raumes betrachtet werden.
Bild
 kalarproduktSkizze.jpg
kalarproduktSkizze.jpgWegen des Kosinussatzes ist die Länge des dem Winkel ³ gegenüberliegenden Vektors
|\vec{c}|^2=|\vec{a}|^2+|\vec{b}|^2-2|\vec{a}||\vec{b}| \cdot \cos(\gamma)
Da sich \vec{c} als \vec{b}-\vec{a} ergibt, erhält man
|\vec{b}-\vec{a}|^2=|\vec{a}|^2+|\vec{b}|^2-2|\vec{a}||\vec{b}| \cdot \cos(\gamma).
Berechnet man nun die Länge über das Skalarprodukt, so erhält man
\left(\vec{b}-\vec{a}\right)\cdot\left(\vec{b}-\vec{a}\right) = \vec{a}\cdot\vec{a} + \vec{b}\cdot\vec{b}-2|\vec{a}||\vec{b}| \cdot \cos(\gamma).
Aus den Rechenregeln für das Skalarprodukt ergibt sich dann
\vec{b}\cdot\vec{b} -2 \vec{a}\cdot\vec{b}+ \vec{a}\cdot\vec{a} = \vec{a}\cdot\vec{a} + \vec{b}\cdot\vec{b}-2|\vec{a}||\vec{b}| \cdot \cos(\gamma)
und daraus die gewünschte Beziehung
\vec{a}\cdot\vec{b} = |\vec{a}||\vec{b}| \cdot \cos(\gamma).
ups--- liess ienfahc selber im wiki nach

Dieser Beitrag wurde bereits 1 mal editiert, zuletzt von »paulo« (16. April 2007, 22:20)
Seraphem
unregistriert
Da war wer schneller 
Aber das soll mal einer verstehen

Vielleicht hilft dir das weiter:
r1 = |r2| * cos(a)
=> r2/|r1| = cos(a)
[Rechengesetz!]
Morgen wird erstmal Mathe Abitur geschrieben ... wenn ich dann noch was davon hören will und du es nicht verstehst, erbarme ich mich vlt und mach ne eigene Zeichnung

Aber das soll mal einer verstehen


Vielleicht hilft dir das weiter:
r1 = |r2| * cos(a)
=> r2/|r1| = cos(a)
[Rechengesetz!]
Morgen wird erstmal Mathe Abitur geschrieben ... wenn ich dann noch was davon hören will und du es nicht verstehst, erbarme ich mich vlt und mach ne eigene Zeichnung

Dieser Beitrag wurde bereits 1 mal editiert, zuletzt von »Seraphem« (16. April 2007, 22:28)
Zur Geometrischen Bedeutung:
Beim Skalarprodukt projiziert man einen Vektor auf einen anderen.
Beispiel:
Man hat einen Vektor a und einen Vektor b
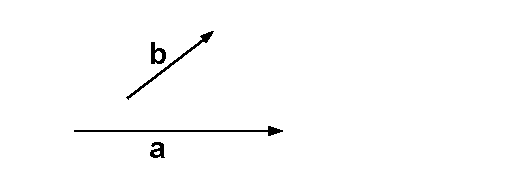
Rechnet man nun a skalar multipliziert mit b (bzw. b skalar multipliziert mit a; es gilt das Kommutatvgesetz), so erhält man einen Betrag, welcher der Länge des projizierten Vektors entspricht.
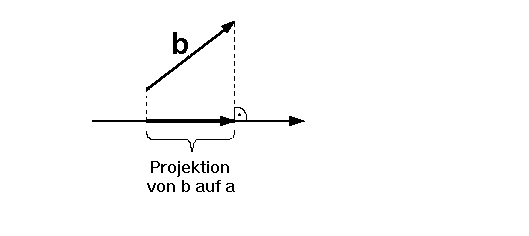
Beim Skalarprodukt projiziert man einen Vektor auf einen anderen.
Beispiel:
Man hat einen Vektor a und einen Vektor b

Rechnet man nun a skalar multipliziert mit b (bzw. b skalar multipliziert mit a; es gilt das Kommutatvgesetz), so erhält man einen Betrag, welcher der Länge des projizierten Vektors entspricht.

" Ein Mensch sollte nie mehr Staub aufwirbeln, als er bereit ist zu schlucken "
Seraphem
unregistriert
Ich hab ihn durchweg dazu kennen gelernt, Senkrechten zu erstellen und beispielsweise Normalenvektoren zu bilden etc...
Du hast uns im Übrigen nicht wirklich nach der Bedeutung sondern danach gefragt, wo deine Gleichung herkommt
Du hast uns im Übrigen nicht wirklich nach der Bedeutung sondern danach gefragt, wo deine Gleichung herkommt

Dieser Beitrag wurde bereits 1 mal editiert, zuletzt von »Seraphem« (17. April 2007, 23:21)


